数学 Math

開球は開集合【証明付き】

開球って本当に開集合でしょうか？

開球は開集合

カイキくん
開球ってホントに「開」なの？
スウガくん
どういう意味だい？
カイキくん
開球って言ってるけどホントに開球は「開集合」なのかなって。
スウガくん
どうしたら納得する？（笑）
カイキくん
開集合の定義通りに示してくれたら、納得する（笑）
スウガくん
OK。じゃあ一緒に証明してみようか。

開球の定義

スウガくん
それじゃあまず開球の定義は覚えている？

カイキくん
覚えてるよ！これでしょ。

[box class="blue_box" title="開球の定義"](X,d) を 距離空間 とする.
x_0\in X, r > 0 とする.
S_r(x_0) = \{x\in X\ |\ d(x, x_0) < r\}
と定義し, S_r(x_0) を「x_0 を中心とする半径 r の開球」という。[/box]
スウガくん
そうそう。いいね。じゃあ次、開集合の定義は？

カイキくん
・・・。なんだっけ？（笑）
スウガくん
（笑）。「距離空間上の開集合の定義と性質」で１回やっているね。もう一回確認しておこう！

開集合の定義

[box class="blue_box" title="開集合の定義"]( X, d ) を距離空間とする。G \subset X とする。
{}^{\forall} x \in G , {}^{\exists}\epsilon > 0 ,{}^{s.t.} S_{\epsilon}(x) \subset G
が成立するとき、  GはXの開集合であるという。[/box]

スウガくん
それじゃあ証明に入ろうか。

カイキくん
はーい

開球は開集合である

S_r(x_0) は X の開集合である.

証明

方針：S_r(x_0) が開集合であることを示すのだから、定義通りに,

{}^{\forall}x\in S_r(x_0), {}^{\exists}\epsilon > 0,{}^{s.t.}S_{\epsilon}(x)\subset S_r(x_0) を示せばよい。

スウガくん
(X,d)は一般の距離空間だけど,前に証明した距離空間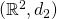(\mathbb{R}^2,d_2) に置き換えて開球の図をかきながら証明を見ると理解しやすいよ。

※　距離空間(\mathbb{R}^2,d_2) の記事はこちら

証明：

{}^{\forall}x\in S_r (x_0) をとる.

S_r (x_0) の定義より,

d(x, x_0) < r.

変形すると, r - d(x, x_0) > 0.

\epsilon = r - d(x, x_0) とおくと,

\epsilon > 0 で, S_{\epsilon}(x) \subset S_r(x_0) である。

実際, y\in S_{\epsilon}(x) とすると,

d(x_0 , y) \le d(x_0, x) + d(x, y)   ( 三角不等式より )

< d(x_0, x) + \epsilon      ( d(x,y) < \epsilon より )

= r - \epsilon + \epsilon     ( \epsilon = r - d(x, x_0)より )

= r

なので, y\in S_r(x_0).

結論：開球 S_r (x_0) は X の開集合である。

-数学 Math
-