n 次元ユークリット空間の定義とノルム空間であることの証明を紹介します。
n次元ユークリッド空間とは
![]() は
は![]() 線形空間であることに注意する.
線形空間であることに注意する.
![]() :
: ![]() を
を ![]()
![]() で定める.
で定める.
このとき, ![]() はノルム空間である.
はノルム空間である.
そして, この空間をn次元ユークリット空間という。
![]() がノルム空間であることを証明するためには,
がノルム空間であることを証明するためには,
![]() がノルムの定義(ノルムの定義はこちら。)を満たしていることを確かめればよい.
がノルムの定義(ノルムの定義はこちら。)を満たしていることを確かめればよい.
(N1), (N2), (N3) の順に示していく.
(N1)
![]()
![]() に対し,
に対し, ![]() で,
で, ![]() を示す.
を示す.
![]() をとる.
をとる.
![]() とかく.
とかく.
このとき,
![]() なので,
なので, ![]() .
.
また,
![]()
![]()
![]()
よって (N1) は示された.
(N2)
![]()
![]() ,
, ![]() に対し,
に対し, ![]() を示す.
を示す.
![]() ,
, ![]() をとる.
をとる.
![]() とかける.
とかける.
このとき,
![]()
![]()
![]()
![]()
![]()
以上より, (N2) は示された.
(N3)
![]()
![]() に対し,
に対し, ![]() を示す。
を示す。
![]() ,
,![]() とかく.
とかく.
![]() は
は ![]() より両辺ともに非負なので,
より両辺ともに非負なので,
両辺を2乗した![]() を示せばよい.
を示せばよい.
![]() (
(![]() の定義より)
の定義より)
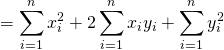
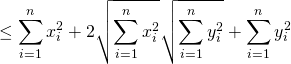 (シュワルツの不等式より)
(シュワルツの不等式より)
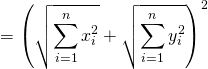
![]() . (
. (![]() の定義より)
の定義より)
以上より, ![]() .
.
以上で, ![]() がノルムの定義を満たしていることわかった.
がノルムの定義を満たしていることわかった.
結論: ![]() はノルム空間である。
はノルム空間である。