-

-
資産運用結果公開 2022/8/16
2022/8/16
現在の投資額 2022/8/16の現在の投資額を公開します。投資の合計額は¥10,557,766となりました。前に書いた2021/5/14の記事のときは、合計額が¥4,416,537でしたので、投資額 ...
-

-
おすすめASPサイト【アフェリエイト】
2022/8/16
ASPとは ASPはApplication Service Provider(アプリケーションサービスプロバイダ)の略です。アフェリエイトサイトを構築するときに登録します。ASPは広告主とサイト運営者 ...
-

-
おすすめニュースアプリ
2022/8/16
こんにちはー。かいきです。通勤がバスで、ずっとyoutubeをみていたんだけど、最近はニュースを見るようになったよ。少しは社会勉強をしないといけないなという気持ちが湧き出てきました。(´・ω・`)使っ ...
-

-
PortFastとは
2021/6/6
PortFastを有効にすると、有効にしたポートでリンクアップしたとき、スパニングツリーのポート状態がブロッキングからフォワーディングに即座に移行します。PortFastが無効になっている場合は、通常 ...
-
-
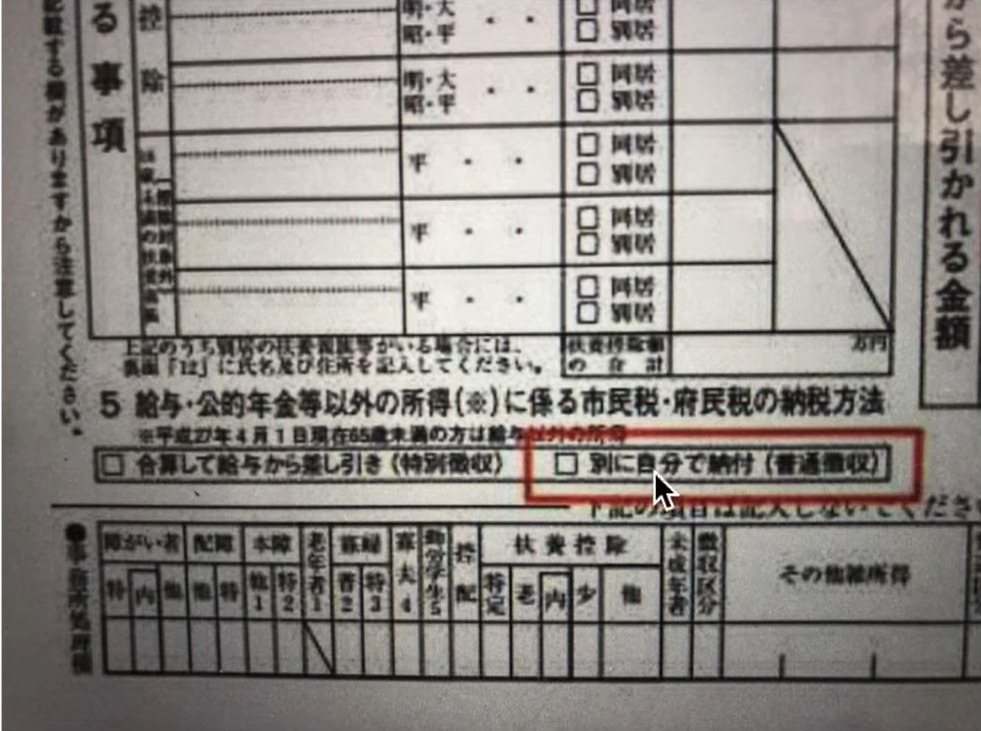
副業が会社にばれないようにする方法
2021/6/6
「副業を始めたいけど、会社では副業を禁止している・・」 「副業は禁止されていないけど、会社の人に知られたくない・・」 そんな人におすすめの記事です。絶対にばれないとは言えませんが、対策を立てることでバ ...
-
-
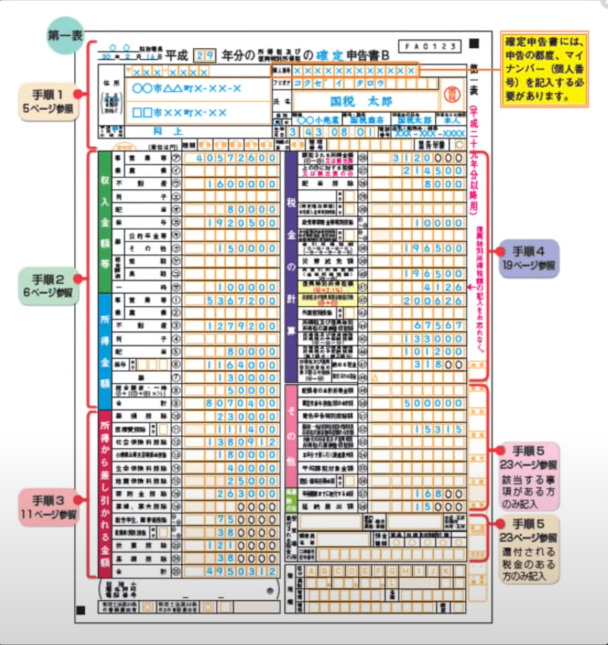
税金の種類
2021/6/6
会社員にかかる税金 会社員にかかる税金は大きく分けて2つあります。所得税と住民税です。 個人事業主にかかる税金 個人事業主にかかる税金は大きく分けて4つあります。所得税、住民税、事業税、消費税です。所 ...
-

-
VOOとは
2021/5/30
VOOの正式名称 VOOの正式名称は、「バンガード・S&P500 ETF」です。VOOという表記は、ティッカーです。ティッカーとは日本株式でいうところの、銘柄コードにあたるもので、米国株式ではアルファ ...
-

-
投資始めました!
2021/5/14
きっかけ 投資をはじめたよ(・∀・)投資ってよく聞くけどよくわからないなーと思っていたので、実際にやってみて学んでいくよ!実際にぼくの投資額も公開していくスタイルにしますっ 現在の投資額 2021/5 ...
-

-
開集合族に関する問題
2020/9/26
開集合族に関する問題を解いてみよう。 開集合族に関する問題 Rの集合族U'={U∈2^R | U∍0}を含む最小の開集合族Uを求め、実際にそうなることを説明してください。 開集合族に関する問題の解答 ...
-

-
『ビジネスフレームワーク図鑑 すぐ使える問題解決・アイデア発想ツール70』【書評】
2022/8/15 BOOKS
『ビジネスフレームワーク図鑑 すぐ使える問題解決・アイデア発想ツール70』を読みました。