開集合ってなーに?
カイキくんは朝が苦手だ。
カイキくんは勉強したことでわからないことがあるとこうやって次の日に質問に来る。
開集合の定義
![]() を距離空間とする。
を距離空間とする。![]() とする。
とする。
![]()
![]()
が成立するとき、 GはXの開集合であるという。
ここで、![]() は
は ![]() で定義しているよ。
で定義しているよ。

![]() 上の任意の元
上の任意の元 ![]() に対して、
に対して、
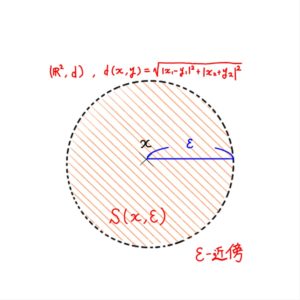
![]() とおいて、
とおいて、
距離を ![]() で定めたときの
で定めたときの
距離空間 ![]() 上での
上での ![]() だね!
だね!
開集合の性質
![]() を距離空間とする。このとき、次の(O1), (O2), (O3)が成り立つ。
を距離空間とする。このとき、次の(O1), (O2), (O3)が成り立つ。
(O1) ![]() 及び
及び ![]() はともに開集合.
はともに開集合.
(O2) 開集合の任意個の和は開集合である。
すなわち、![]() が開集合
が開集合 ![]()
![]() は開集合.
は開集合.
(O3) 有限個の開集合の共通部分は開集合である。
すなわち、![]() が開集合
が開集合 ![]() は開集合.
は開集合.
証明
(O1).
まず、![]() とる。
とる。
![]() より、
より、![]() は
は ![]() の開集合である。
の開集合である。
次に、![]() が
が ![]() の開集合であることを示す。
の開集合であることを示す。
そのためには、「![]() 」が真であればよい。
」が真であればよい。
![]() は成立しないので、「
は成立しないので、「![]() 」は正しい。
」は正しい。
よって、![]() は
は ![]() の開集合である。
の開集合である。
(O2).
![]() とおき、
とおき、![]() とする。
とする。
![]() だから、和集合の定義より、
だから、和集合の定義より、![]() となる
となる ![]() が存在する。
が存在する。
仮定より、![]() は開集合であるから,
は開集合であるから, ![]() となる
となる ![]() が存在する。
が存在する。
![]() .
.
よって、![]() は
は ![]() の開集合である。
の開集合である。
(O3).
![]() とする.
とする.
共通部分の定義より、![]()
![]() であり、
であり、
すべての ![]() は
は ![]() の開集合であるから、各
の開集合であるから、各 ![]() に対して、
に対して、
![]() となる
となる ![]() が存在する。
が存在する。
![]() とおくと、
とおくと、
![]()
![]() であるから,
であるから,
![]()
したがって、![]() は
は ![]() の開集合である. □
の開集合である. □


