平面上の開集合の表現
![]() を開区間とする.
を開区間とする.![]() とおく.
とおく.![]() 内の任意の開集合
内の任意の開集合![]() はこの
はこの![]() のような形をした
のような形をした![]() の可算個の和集合で表される。
の可算個の和集合で表される。
証明
![]() を
を![]() の開集合とする.
の開集合とする.
![]() のすべての有理点を
のすべての有理点を![]() とし,
とし,
またすべての正の有理数を![]() とする.
とする.
![]() とおく.
とおく.
![]() とおく.
とおく.
![]() をとる.
をとる.![]() は開集合なので、開集合の定義より
は開集合なので、開集合の定義より
![]() .
.
すべての有理点![]() は
は![]() で稠密なので,
で稠密なので,
![]() となる
となる![]() が存在.
が存在.
また,![]() となる
となる![]() が存在.
が存在.
![]() だから,
だから,
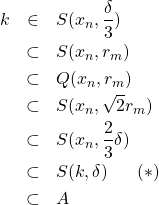
ゆえに,![]() .
.
![]() に含まれる
に含まれる![]() は存在する.
は存在する.
![]() に含まれる
に含まれる![]() 全体を
全体を
![]() と表せば,
と表せば,
![]()
逆の包含関係は明らかなので![]() .
.
![]()
![]() をとる.
をとる.
![]() .
.
ゆえに![]() .
.