収束する数列と積の関係を紹介します。
数列の収束と積
2つの収束する数列![]() と
と![]() があるとき、この2つの積からなる数列
があるとき、この2つの積からなる数列![]() はどこに収束するだろうか?
はどこに収束するだろうか?
![]() 上では、
上では、![]() のとき、
のとき、
![]() が成立することが分かっています。
が成立することが分かっています。
つまり、![]() は
は![]() と
と![]() の極限の積に収束するということです。
の極限の積に収束するということです。
性質
![]() において、実数列
において、実数列 ![]() と
と ![]() が
が
![]() を満たすとき、
を満たすとき、
![]() .
.
証明
収束する数列は有界だから、有界の定義より、
![]() が成り立つ。
が成り立つ。
ここで、![]() について、場合分けをしてそれぞれについて証明していく。
について、場合分けをしてそれぞれについて証明していく。
(i)![]()
(ii)![]() の2通りに分ける。
の2通りに分ける。
まず、 (i) 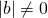 の場合を考える。
の場合を考える。
任意の正の数![]() をとる。
をとる。
![]() より、
より、
![]() .
.
![]() より、
より、
![]() .
.
![]() とおく。
とおく。
![]() のとき、
のとき、
![]()
![]()
![]()
![]()
![]()
![]() .
.
ゆえに、![]()
次に、 (ii) 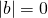 の場合を考える。
の場合を考える。
「![]() 」に注意する。
」に注意する。
任意の正の数![]() をとる。
をとる。
![]() より、
より、
![]() .
.
![]() のとき
のとき
![]()
![]()
![]()
![]()
![]() .
.
ゆえに、![]()
(i),(ii)より、題意は示された。 □