数学 Math

集合（ 和集合、共通部分、部分集合 ）

よく使う集合の表記法や和集合、共通部分、部分集合、集合として等しいことの定義を紹介する。

よく使う集合の表記法

\mathbb{N} とかいて自然数全体のなす集合をあらわす。\mathbb{N} = \{\ 1,2,3,4,5,\cdots\ \}

\mathbb{Z} とかいて整数全体のなす集合をあらわす。\mathbb{Z} = \{\ \cdots,-2,-1,0,1,2,\cdots\ \}

\mathbb{Q} とかいて有理数全体のなす集合をあらわす。\mathbb{Q} = \{\ \frac{q}{p}\ |\ p\in\mathbb{N},q\in\mathbb{Z}\ \}

\mathbb{R} とかいて実数全体のなす集合をあらわす。

\mathbb{C} とかいて複素数全体のなす集合をあらわす。\ \mathbb{C} = \{a + bi \ |\ a,b \in\mathbb{R}\ \}

定義（和集合と共通部分）

和集合

A, B を集合とする。

A \cup B = \{\ x\ |\ x\in A\ または\ x\in B\ \}.

とかき、A \cup B を A と B の和集合という。

一般に：

\displaystyle\bigcup_{n=1}^{\infty} A_n = \{\ x\ |\ {}^{\exists}n\in\mathbb{N}, {}^{s.t.}x\in A_{n}\ \}

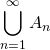
「x \in A \cup B」 \Leftrightarrow 「 x\in A または x\in B 」となるよ。

共通部分

A, B を集合とする。

A \cap B = \{\ x\ |\ x\in A\ かつ\ x\in B\ \}.

とかき、A \cap B を A と B の共通部分という。

一般に：

\displaystyle\bigcap_{n=1}^{\infty} A_n = \{\ x\ |\ {}^{\forall}n\in\mathbb{N}に対し, x\in A_{n}\ \}

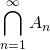
定義（部分集合, 等しい集合）

部分集合

A, B を集合とする。

x\in A \Rightarrow x\in B が成立するとき,

A は B の部分集合であるといい, A \subset B ( または、A \supset B )　で表す。

「集合として等しい」とは

A, B を集合とする。

A \subset B かつ A \supset B

が成立するとき、A と B は等しい といい, A = B で表す。

-数学 Math
-