位相空間の定義【距離空間からつくられる位相空間】

位相空間の定義を確認し、距離空間から自然につくられる位相空間とその証明を紹介します。

定義（位相空間）

を集合とし、
をのいくつかの部分集合からなる族とする。このとき次の が成り立つならを位相といい、を位相空間という

距離空間からつくられる位相空間

を距離空間とする。
 を の開集合全体の族とするとき,
は位相空間となる.

証明

方針：

が位相空間となることを示すので, 位相の定義における
位相の条件 を満たすことを示せばよい。

また,すべての条件において, 開集合の性質を使うので,
「距離空間上の開集合の性質」を参照する。

証明：

を距離空間とし, を の開集合全体の族とする。

は の開集合であるから,.

も の開集合であったから, .

任意個の開集合 に対し,

任意個の開集合の和集合は開集合であるので, .

有限個の開集合 に対し,

有限個の開集合の共通部分は開集合だから,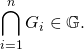

結論：

位相の条件 を満たしたので, は位相空間である。