「ワルツをマスターしたい」
シュワルツの不等式とカイキくん。
シュワルツの不等式とカイキくん
カイキくん
ワルツをマスターしたい。
スウガくん
ダンスでも踊るのかな?
シュワルツの不等式
![]() を実数とする. このとき,
を実数とする. このとき,
![Rendered by QuickLaTeX.com \[ (\ \sum_{i =1}^n a_i b_i\ )^2 \le (\ \sum_{i =1}^n a_i^2\ ) (\ \sum_{i =1}^n b_i^2\ ) \]](https://kaikiblog.com/wp-content/ql-cache/quicklatex.com-883966bb8e3ff127b8337b1bfcfed299_l3.png)
.
スウガくん
Σがない形で書いてみよう!理解が深まるかも!
Σがない形で不等式の部分をかくと,
![]()
![]()
になるよ。
証明
![]() を実数とし,
を実数とし, ![]() とする.
とする.
各 ![]() に対して,
に対して, ![]() より、
より、
![]() (※)
(※)
さらに,
![]()
![]()
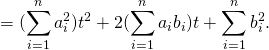
これを ![]() に関する 2 次関数とみると, 下に凸なグラフでかける.
に関する 2 次関数とみると, 下に凸なグラフでかける.
また (※) より, グラフは ![]() 軸と共有点を持たないかまたは接している.
軸と共有点を持たないかまたは接している.
すなわちこれは, 判別式 ![]() の場合である.
の場合である.
よって,
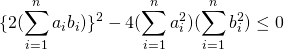 .
.
さらに, 4で割って, 移項すると
![]() . □
. □

