全射、単射、全単射の定義と[0,1) から (0,1) への全単射写像をつくる方法を紹介する。
全射と単射、全単射
全射の定義
![]() を写像とする。
を写像とする。
任意の ![]() に対して、
に対して、![]() となる
となる ![]() が存在するとき、
が存在するとき、
![]() は全射であるという。
は全射であるという。
つまり、記号で書くと、
![]() が成立することです。
が成立することです。
単射の定義
![]() を写像とする。
を写像とする。
![]() が成立するとき、
が成立するとき、
![]() は単射であるという。
は単射であるという。
全単射の定義
![]() を写像とする。
を写像とする。
![]() が全射かつ単射であるとき、
が全射かつ単射であるとき、![]() は全単射であるという。
は全単射であるという。
全単射は、双射、上への1対1写像、一対一対応などともいいます。
本によって呼ばれ方が変わるので、覚えておくと便利です。
[0,1) から (0,1) への全単射写像
問. [0,1) から (0,1) への写像で全単射となる写像をつくれ。
解答例
写像 ![]() を
を
(1) 
で定める。
このとき、この ![]() が
が ![]() から
から ![]() への全単射写像であることを示す。
への全単射写像であることを示す。
全単射写像は全射かつ単射の写像でした。
なので、
- 全射であること
- 単射であること
をそれぞれ確かめてみよう。
(全射であること)
![]() をとる。
をとる。
![]()
![]() のとき、
のとき、
![]() とおくと、
とおくと、![]() .
.
![]()
![]() のとき、
のとき、
![]() となる
となる ![]() が存在する。
が存在する。
![]() とおくと、
とおくと、![]() .
.
![]()
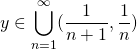 のとき、
のとき、
![]() とおくと、
とおくと、![]() .
.
よって、以上より、![]() は全射である。
は全射である。
(単射であること)
![]() とする。
とする。
![]()
![]() のとき、
のとき、
![]() となる
となる ![]() が存在する。
が存在する。
![]() .
.
よって、![]() .
.
![]()
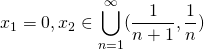 のとき、
のとき、
![]() .
.
![]() の取り方より,
の取り方より, ![]()
![]()
なので、![]()
よって、![]() .
.
![]()
![]() のとき、
のとき、
![]() となるような
となるような ![]() が存在。
が存在。
![]() となるような
となるような ![]() が存在。
が存在。
![]() より,
より, ![]() .
.
![]() .
.
![]() .
.
![]()
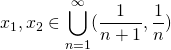 のとき、
のとき、
![]() .
.
![]() より、
より、![]() .
.
![]()
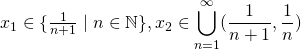 のとき、
のとき、
![]() となるような
となるような ![]() が存在する。
が存在する。
![]()
ここで、![]() とおくと、
とおくと、![]() は自然数なので、
は自然数なので、
![]()
![]()
![]()
である。
![]() の取り方より、
の取り方より、![]() .
.
よって、![]() .
.
以上より ![]() は単射である。
は単射である。
全単射写像と濃度
また、これは[0,1) と(0,1) の濃度が等しいことを表しています。
濃度が等しいことの定義と、全単射写像の他の例を見てみたい方はサイト内で探してみてね。