ハイネ・ボレル（Heine-Borel）の被覆定理

ハイネ・ボレルの被覆定理

ハイネ・ボレルの被覆定理

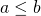$a \le b$ , $a,b\in \mathbb{R}$ とする。

有界閉区間 $[a,b]$ はコンパクトである。

証明しよう

証明の方針：

$[a,b]$ がコンパクトであることを示す。

定義通りに示すなら、
$[a,b]$ の任意の開被覆 $\{ G_{\mu}\}$ に対して、
その中の適当な有限個 $G_{\mu_1},\cdots,G_{\mu_n}$ を選んで、
$[a,b] \subset \displaystyle\bigcup_{i = 1}^{n} G_{\mu_i}$ とできることをいえばよい。

背理法で示す。

$\{ G_{\mu}\}$ を $[a,b]$ の任意の開被覆とし、
どんな有限個の開被覆 $G_{\mu_1},\cdots,G_{\mu_n}$ を選んでも、
$[a,b] \not\subset \displaystyle\bigcup_{i = 1}^{n} G_{\mu_i}$ となると仮定する。

このとき、矛盾がでることをいえばよい。

証明：

背理法で示す。

$\{ G_{\mu}\}$ を $[a,b]$ の任意の開被覆とする。

[a,b] は $\{G_{\mu}\}$ のうちの有限個では覆えないと仮定する。

$c = \frac{a + b}{2}$ とおく。

すると、 $c$ は閉区間 $[a,b]$ を２等分する点である。

閉区間 $[a,b]$ は $\{G_{\mu}\}$ のうちの有限個では覆えないので、
$[a,c]$ と $[c,b]$ のうちで少なくともどちらか一方は $\{G_{\mu}\}$ のうちの有限個で覆えない。

[aside type="normal"]
なぜなら、 $[a,c]$ と $[c,b]$ の両方とも $\{G_{\mu}\}$ のうちの有限個で覆えるとすると、

$[a,b]$ が $\{G_{\mu}\}$ のうちの有限個で覆えることになってしまい、仮定に矛盾するからである。
[/aside]
$[a,c]$ と $[c,b]$ のどちらとも $\{G_{\mu}\}$ のうちの有限個で覆えない場合は、 $[a,c] = [a_1, b_1]$ とし、

$[a,c]$ と $[c,b]$ の片方のみ $\{G_{\mu}\}$ のうちの有限個で覆えない場合は、その $\{G_{\mu}\}$ のうちの有限個で覆えないほうを $[a_1, b_1]$ とおく。

さらに、 $[a_1, b_1]$ を２等分して２つの閉区間を考えると、

同じように、そのうちで少なくともどちらか一方は $\{G_{\mu}\}$ のうちの有限個で覆えない。

そして、先ほどと同様に、 $[a_2,b_2]$ を定義する。

この操作を繰り返す。すると、

[box class="glay_box"] $[a_1,b_1] \supset [a_2,b_2] \supset [a_3,b_3]\supset\cdots$

となる有界閉区間の列 $\{[a_i,b_i]\}_{i = 1}^{\infty}$ がとれる。[/box]

区間の幅を考えると、 $a_n,b_n$ のとり方より、

$b_n - a_n = \frac{1}{2^n}(b - a)$

$\to 0$ ( $n \to \infty$ ).

カントールの区間縮小法より、
$\displaystyle\lim_{n \to \infty} a_n =\displaystyle\lim_{n \to \infty} b_n = x_0$
となる $x_0 \in [a,b]$ が存在する。

$[a,b] \subset \displaystyle\bigcup_{\mu} G_{\mu}$ なので、
$x_0 \in G_{\mu_0}$ となる $\mu_{0}$ が存在。

$G_{\mu_0}$ は $\mathbb{R}$ の開集合であるから、
${}^{\exists}\epsilon > 0, S_{\epsilon}(x_0) \subset G_{\mu_0}$

$\displaystyle\lim_{n \to \infty} a_n =\displaystyle\lim_{n \to \infty} b_n = x_0$ なので、
$[a_{n_0},b_{n_0}] \subset S_{\epsilon}(x_0)$ となるように $n_0\in \mathbb{N}$ がとれる。