はじめに
この記事では、コンパクトではない集合の例を示し、その証明方法を紹介します。
記事「有限集合はコンパクトである。(開被覆とコンパクト)」では、コンパクトの定義とコンパクトである集合の例を挙げて示しました。
では、コンパクトでない集合の例にはどのようなものがあるでしょうか。
また、その証明方法について学んでいただければ幸いです。
コンパクトではない集合
![]() の部分集合
の部分集合 ![]() は
は
![]() において, コンパクトではない。 これを示せ。
において, コンパクトではない。 これを示せ。
方針:
コンパクトではないことを示せばよいので、コンパクト集合の定義の否定をつくる。
「![]() のある開被覆に対しては、その中からどんなふうに有限個の開集合をとってきても、
のある開被覆に対しては、その中からどんなふうに有限個の開集合をとってきても、![]() を覆うようにできない」
を覆うようにできない」
ということを示せばよい。
解:
各 ![]() に対し、
に対し、
![]() とおくと、
とおくと、
各 ![]() は
は ![]() における開集合である。
における開集合である。
![]()
![]()
![]()
![]() であるから、
であるから、
![]() は
は ![]() の開被覆である。
の開被覆である。
有限個の開集合 ![]()
![]() を任意にとる。
を任意にとる。
ここで, ![]() とおく。
とおく。
![]()
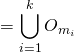 である。
である。
一方で, ![]()
よって, 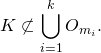
結論:
![]() はコンパクトではない。
はコンパクトではない。