この記事では、開被覆、コンパクトの定義を確認し、有限集合はコンパクトであるということを示します。
定義(開被覆)
![]() を位相空間とする。
を位相空間とする。
![]() に対して,
に対して,
![]() かつ
かつ ![]()
を満たす集合族 ![]() を
を ![]() の開被覆であるという。
の開被覆であるという。
定義 ( コンパクト)
![]() を位相空間とし,
を位相空間とし, ![]() を
を ![]() の部分集合とする。
の部分集合とする。
K の任意の開被覆 ![]() に対し,
に対し,
その中の適当な有限個 ![]() を選んで,
を選んで,
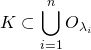 とできるとき,
とできるとき,
![]() は コンパクトであるという。
は コンパクトであるという。
有限集合はコンパクトである。( コンパクト集合の例 )
![]() を位相空間とする。
を位相空間とする。
![]() の有限集合はコンパクトであることを示せ。
の有限集合はコンパクトであることを示せ。
解:
![]() 内の有限集合を,
内の有限集合を,![]() で表す。
で表す。
![]() とおく。
とおく。
![]() を
を ![]() を満たす開集合族とする。
を満たす開集合族とする。
![]() より,
より,
各 ![]() に対して,
に対して,
![]() .
.
よって, 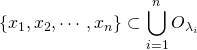 .
.
したがって, ![]() はコンパクトである。
はコンパクトである。
結論:
位相空間の有限集合はコンパクトである.