ベクトル空間の定義と基本的な性質の証明の紹介。
線形空間(ベクトル空間)の定義
- 線形空間
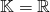 or
or 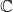 とする. 集合
とする. 集合 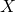 の元に対し,
の元に対し,
和:
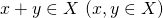 ,
,
スカラー倍: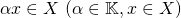
が定まり, 以下の8つの条件を満たすとき,
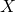 を
を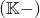 線形空間という。
線形空間という。
また,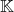 を線形空間
を線形空間 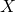 の係数体という.
の係数体という.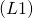
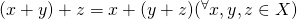
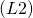
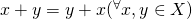
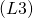
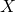 の元
の元  が存在して,
が存在して, 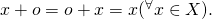
この元 をゼロベクトルという.
をゼロベクトルという.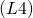
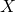 の任意の元
の任意の元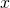 に対して,
に対して,
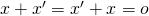 となる
となる 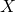 の元
の元 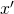 が存在する.
が存在する.
この元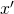 を
を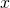 の逆ベクトルといい,
の逆ベクトルといい, 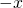 とかく. :
とかく. :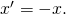
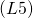
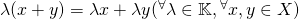
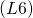
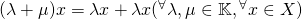
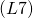
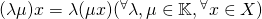
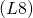
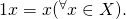
線形空間の簡単な性質
![]() を
を![]() 線形空間とする。
線形空間とする。
① ゼロベクトル![]() はただ1つに限り存在する.
はただ1つに限り存在する.
② ![]() が成立する.
が成立する.
証明
①
![]() をゼロベクトルとする.
をゼロベクトルとする.
背理法で示す.
![]() となるゼロベクトル
となるゼロベクトル ![]() が存在するとする.
が存在するとする.
![]() で
で![]() はゼロベクトルだから,
はゼロベクトルだから, ![]() より,
より,
![]() (※1)
(※1)
一方で![]() で
で![]() もゼロベクトルだから,
もゼロベクトルだから, ![]() より,
より,
![]() (※2)
(※2)
(※1) と(※2)を合わせて, ![]()
これは, ![]() に矛盾する.
に矛盾する.
よって, ![]() となるゼロベクトル
となるゼロベクトル ![]() は存在しない.
は存在しない.
すなわち, ゼロベクトル![]() はただ1つに限り存在する.
はただ1つに限り存在する.
②
![]() とする. スカラー倍で閉じているから,
とする. スカラー倍で閉じているから, ![]() であることに注意する.
であることに注意する.
![]() と
と![]() より,
より, ![]() となる
となる ![]() の逆元
の逆元 ![]() が存在する.
が存在する.
つまり, ![]() .
.
さらに,
![]()
![]() (
( ![]() 上で
上で![]() より )
より )
![]() (
(![]() より )
より )
![]() (
(![]() より )
より )
![]() (
( ![]() より )
より )
![]() (
( ![]() より ).
より ).
以上より, ![]() . □
. □