離散距離空間(証明付き)
![]()
![]() ) 上の任意の元
) 上の任意の元 ![]() に対して、
に対して、
(1) 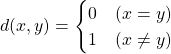
で定める。
このとき, ![]() は距離空間である。
は距離空間である。
スウガくん
この距離空間には離散距離空間という名前がついているよ。
証明
![]() をとる。
をとる。
![]()
![]() なので,
なので, ![]() はよい.
はよい.
また, ![]() の定義の仕方から,
の定義の仕方から, ![]() で,
で,
![]() のとき, 仮に
のとき, 仮に ![]() であるとすると,
であるとすると, ![]() となって矛盾する.
となって矛盾する.
よって, ![]()
合わせて, ![]()
![]()
![]() のとき,
のとき, ![]() .
.
![]() のとき,
のとき, ![]() .
.
よって, ![]() .
.
![]()
![]() は 0 か 1 のみを値にとるので、
は 0 か 1 のみを値にとるので、
![]() と
と ![]() で場合分けして考える.
で場合分けして考える.
![]() のときは、
のときは、![]() の定義より,
の定義より, ![]() .
.
![]() のとき,
のとき, ![]() より, 「
より, 「 ![]() または
または ![]() 」 である。
」 である。
実際, 仮に 「 ![]() かつ
かつ ![]() 」 とすると,
」 とすると, ![]() となり,
となり, ![]() に矛盾する.
に矛盾する.
よって, 「 ![]() または
または ![]() 」なので,
」なので, ![]() .
.
ゆえに, ![]() . □
. □
