ユークリッド空間は距離空間
![]() 上の任意の元
上の任意の元 ![]() に対し、
に対し、
![]() ,
, ![]() とおく。
とおく。
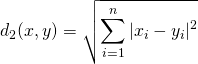 で定める。
で定める。
![]() は距離空間である。
は距離空間である。
証明
![]() が距離の定義を満たしていることを確認していけばよい。
が距離の定義を満たしていることを確認していけばよい。
![]() をとる。
をとる。![]() ,
, ![]() ,
, ![]() で表す。
で表す。
![]()
平方根の定義より, 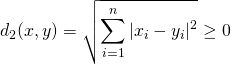 である.
である.
また,
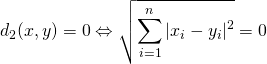
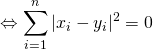
![]()
![]()
![]()
![]()
![]()
![]() .
.
以上より, ![]() .
.
![]()
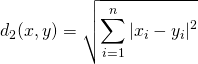
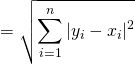
![]()
以上より, ![]()
![]()
![]() に対し、
に対し、
![]() とおくと、
とおくと、
![]() である。
である。
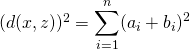
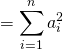
![]()
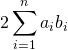
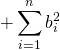
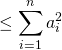
![]()
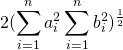
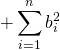 (シュワルツの不等式より)
(シュワルツの不等式より)
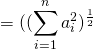
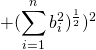
![]()
以上より, ![]() .
.
結論:![]() を満たしたので,
を満たしたので, ![]() は
は ![]() 上の距離であり,
上の距離であり, ![]() は距離空間である.
は距離空間である.
豆知識
ユークリッド空間が距離空間の定義を満たすのは当たり前です。
なぜなら、今回導き出したこのユークリッド空間の性質から取り上げて抽象化してできたものが距離空間だからです。