こんにちは!かいきです。
今回は、実数の例と定義、複素数との違い、について見ていきましょう。
実数の例(0,自然数,…)を知る

例(0,自然数など)
0は実数です。
他にも、1,2,3,-3,1.5,1/3,√2,π,…などの例があるよ。
数直線上で表される数はすべて実数であると思っておくと大丈夫。
ちなみに、実数は有理数と無理数に分けられるよ。
0は有理数です。
1,2,3,-3,1.5,1/3もすべて有理数の例。
√2,πは2つとも無理数。
さらに細かく分けると、
有理数は、自然数と0、負の整数、有限小数、循環小数に分けられます。
無理数は、超越数と超越数でない数に分けられるよ。
上の例でいうと、
1,2,3は自然数。
-3は負の整数。
1.5は有限小数。
1/3=0.333…は循環小数。
πは超越数で、√2は超越数でない数だよ。
実数でないもの
1+2iは実数ではありません。
ここで、iはi2=-1をみたす数のことです。
このiは虚数単位と呼ばれています。
複素数と実数の違い
複素数と実数の違いは、iによって生じます。
iは複素数に現れます。
複素数とはどんな数なのか見てみましょう。
複素数は、(実数)+(実数)i という形で表せる数です。
たとえば、1+2i、3i+2、2i、2が複素数。
理由は下記のようになります。
[box class="glay_box"]1+2i
(1も2も実数。(実数)+(実数)i という形です。)
3i+2
(これも複素数です。3i+2=2+3iですから、上の複素数の形にできましたね。)
2i
(これも複素数。2i=0+2iとかけるからです。)
2
(これも複素数です。2=2+0iとかけます。)[/box]
「あれ?2って実数だよね?」って思ったあなたは正解です。
2は確かに実数。そして複素数でもあるということになります。
実は、実数はすべて複素数です。
先ほどと同じようにやれば、どんな実数でも、(実数)=(実数)+0iとかけるからです。
一方で、複素数は実数とは限りません。
1+2iがその一例です。

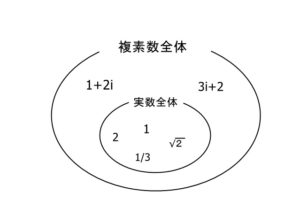
上の図では、複素数と実数の包含関係を表しています。
1+2iの位置に注目してください。
こんなふうに、図で表すと関係が理解しやすくなります。
見つけた数字を図に書き込んでいく作業とかも面白いかもしれませんね。
実数の定義を知る

実数とは何か、という問いへの適切な答えは、
高校までの数学と大学数学で変わってきます。
順に見ていきましょう。
高校まで
高校までは、実数を有理数と無理数の総称としてとらえます。
数直線をイメージして、その上の点は実数だと理解していれば大丈夫です。
大学数学では
大学数学では、
自然数の公理系(ペアノの公理系)から始めて、
自然数→整数→有理数→実数
と順次構成し、実数を定義することができます。
私は一度これを、ペアノの公理から勉強しましたが、
かなり時間はかかりました。本1冊分です。
だけど、その時間に見合った感動はあったかな(笑)
自然数という単純な数のみから、
自然数→整数→有理数→実数の順に構成していき、数の種類が増えていくんです。
その1つ1つがワクワクします。
バラバラに理解していたものが、1つの考えに統合される感じです。
あと、構成の仕方も、「そういう風にやるのか―」って感じで僕にとっては新鮮でした。
実際に自然数からの構成をしてみたい方はこちらの本がオススメです。
リンク先の商品説明の欄に、目的別勉強順という項目があります。
そこで、ペアノの公理からの構成を学びたい人が
どんな順番で読んでいけばよいか書いてあります。
その順番で読み進めていくと理解が速いです。
また、解析学系の本では、実数の公理系から始める本がほとんんどです。
なぜなら、ペアノの公理系からはじめると時間がかかりすぎるからです。
微分積分学の勉強をするために、実数論を勉強する人もいると思います。
そんな方は、ペアノの公理系からではなく、実数の公理系から始めるのがオススメ。
このタイプのオススメの本はこちらです。
この本は、厳密に書かれていて行間をほとんど考えることなく読めるので、すごく読みやすいです。
特に、連続性の公理に疑問を持っている方にもお勧めできる内容でした。
興味があれば、こちらの記事で少し「連続性の公理」について触れているので、読んでみてね。
完備距離空間と例【連続性の公理】
今回の話題に関連する書籍を2冊、紹介しました。
自分の勉強の目的に合わせて本を選んでくださいね!
以上です。

