数学 Math

濃度の定義と同じ濃度をもつ集合の例【証明付き】

濃度の定義、同じ濃度をもつ集合の例とその証明を紹介する。

集合の濃度

A, B を集合とする。

A から B への全単射写像が存在するとき,  A と B は対等であるといい,

A \sim B であらわす。

A と B が対等であるとき、A と B は同じ濃度をもつといい,

card\ A = card\ B であらわす。

同じ濃度をもつ集合の例

S^1 = \{\ (x,y)\in\mathbb{R}^2 \mid x^2 + y^2 = 1\ \} とし、

[0,1] = \{\ x \in \mathbb{R} \mid 0 \le x \le 1\ \} とする。

このとき, card\ S^1 = card\ [0,1] を示せ.

証明の方針：

写像 f : S^1 \to [0,1] で全単射写像となるものを見つければよい。

証明：

写像 f : S^1 \to [0,1] を

(1)   \begin{equation*} f((x,y)) = \begin{cases} \frac{y}{4} + \frac{1}{4} & (x \ge 0) \\ \frac{y}{4} + \frac{3}{4} & (x < 0) \end{cases} \end{equation*}

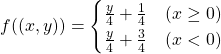
で定める。

このとき、この f は全単射写像である。

（全射性）

方針：

{}^{\forall} z \in [0,1] に対して, f((x,y)) = z となる (x,y)\in S^1 が存在することを確認すればよい。

解：

{}^{\forall} z \in [0,1] をとる。

(i) z \in (\frac{1}{2},1] のとき、

x = - \sqrt{24z -16z^2 -8}\ ,\ y = 4z - 3 とおけば,

x^2 + y^2 = 1 であるから、

(x,y) \in S^1.

そして、f((x,y)) = \frac{4z - 3}{4} + \frac{3}{4} = z.

(ii) z\in [0,\frac{1}{2}] のとき、

x =\sqrt{8z - 16z^2}, y = 4z -1 とおけば,

x^2 + y^2 = 1 であるから、

(x,y) \in S^1.

そして、f((x,y)) = \frac{4z - 1}{4} + \frac{1}{4} = z.

したがって, f は全射である。

（単射性）

方針：

(x,y), (x',y')\in S^1 とし、f((x,y)) = f((x',y')) とする。このとき, (x,y) = (x',y') であることを示せばよい。

解：

(x,y), (x',y')\in S^1 かつ f((x,y)) = f((x',y')) とし、

f((x,y)) = f((x',y')) = \alpha とおく。

(i) 0 \le \alpha \le \frac{1}{2} のとき、

\frac{y}{4} + \frac{1}{4} = \frac{y'}{4} + \frac{1}{4}

y = y'.

x^2 + y^2 = 1 かつ (x')^2 + (y')^2 = 1 で,

y = y' なので,

x^2 - 1 = (x')^2 - 1

x^2 - (x')^2 = 0

(x + x')(x - x') = 0

x + x' = 0 または x - x' = 0

x + x' = 0 のとき、

x, x' \ge 0 より, x = 0 = x'.

x - x' = 0 のとき、

x = x'.

以上より, (x,y) = (x', y').

(ii) \frac{1}{2} < \alpha \le 1 のとき,

\frac{y}{4} + \frac{3}{4} = \frac{y'}{4} + \frac{3}{4} より

y = y'.

x^2 + y^2 = 1 かつ (x')^2 + (y')^2 = 1 で,

y = y' なので,

x^2 - 1 = (x')^2 - 1

x^2 - (x')^2 = 0

(x + x')(x - x') = 0

x,x' < 0 より x + x' \neq 0 なので、

x - x' = 0.

よって, x = x'.

したがって, (x,y) = (x', y').

以上 (i) , (ii) より、f は単射である。

以上を合わせて, f が全単射写像であることが分かった.

結論：card\ A = card\ B 。

-数学 Math
-